Valjak - pojam, elementi, preseci
Ove školske godine smo obrađujući geometrijska tela prvo učili prizme, zatim piramide i sad su nam na red došla obrtna tela u koje spadaju valjak, kupa i lopta. Zašto se zovu obrtna tela? Zato što nastaju obrtanjem nekih geometrijskih figura (valjak - pravougaonika, kupa - trougla i lopta - kruga). Pokazaćemo sve to na narednim časovima.
Za početak, radimo valjak. Svi znamo kako valjak izgleda i viđate svakodnevno predmete valjkastog oblika. Ono što treba da primetimo je da nas valjak podseća na prizmu (pa će imati i neke slične formule), kupa na piramidu. Zašto valjak ipak nije prizma? Zato što valjak u osnovi ima krug a po definiciji, prizme u osnovi imaju mnogouglove.
Kako nastaje valjak?
Valjak nastaje od valjkaste tj. cilindrične površi koja je poprečno presečena dvema paralelnim ravnima. Sve vreme pominjem prizmu, ali sećate se da smo tako rekli da nastaje i prizma, od prizmatične površi. Cilindričnu površ zamišljamo kao jednu beskonačno dugačku cev i nju presecamo dvema paralelnim ravnima. Ti preseci će biti krugovi, osnove valjka, a deo cilindrične površi između osnova predstavlja omotač valjka.
Videli ste već u video lekciji (03:04) kako nastaje cilindrična površ, rotacijom jedne prave oko neke već zadate, ose rotacije, koja će predstavljati i osu simetrije tog valjka. Ako je ta osa normalna na osnovu valjka dobijamo prav valjak, u suprotnom je valjak kosi.
Na slici dole možemo videti visinu valjka, H, koja predstavlja udaljenost centara krugova koji su osnove, poluprečnik osnova, r, i izvodnicu, s, koja je u stvari jednaka sa H.
Sad bi bilo dobro da otvorite ovaj link i da pogledate ali i nacrtate kod sebe u svesku sve načine kako od ovog pravougaonika sa stranicama 2 cm i 4 cm može nastati valjak i da za svaki crtež odredite r i H. Koristite klizač alfa koji pokazuje do kog stepena ste stigli rotacijom.
Zatim otvorite i naredni odeljak gde su vam prikazani elementi valjka koji će vam se prikazati ako ih označite. Valjak sa desne strane čak možete da okrećete i gledate iz različitih uglova. Ko kaže da učenje mora biti dosadno? 😀 Istražite i sami ponešto.
Sledeće što treba da uočimo je osni presek (i njega vidite u sledećem odeljku istog linka).
Osni presek je kod pravog valjka pravougaonik kojeg dobijate kada biste uzduž presekli valjak kroz osu (zato se zove osni presek). Taj pravougaonik za stranice ima prečnik kruga i visinu (izvodnicu tačnije ali smo već rekli da su iste dužine) pa ćemo njih i množiti da bismo odredili površinu osnog preseka. Osni presek na sledećoj slici vidite kao žuti pravougaonik i primetićemo i dijagonalu koja je nacrtana tom pravougaoniku za čije izračunavanje ćemo da iskoristimo Pitagorinu teoremu pa prepišite u vaše sveske bitne formule i skicirajte sliku. Naravno da nema potrebe da učimo to sve napamet, u svakom zadatku možete nacrtati sliku i ako znamo šta tražimo, umećemo da izvedemo sami formule.
Još jedan od preseka na koje možete naići u zadacima i pomenut je u lekciji je poprečni ili paralelni presek i nije ništa drugo nego krug podudaran krugu u osnovi i njegovu površinu računamo po formuli:
ovde je B, naravno, oznaka za površinu baze.
Osim što imate za domaći da sami izvučete iz lekcije najbitnije i nacrtate nastajanje valjka rotacijom, imate i da uradite koji zadačić iz vaše školske zbirke sa strane 117. Zadaci su: 3, 4, 5, i 7.
Još jedan od preseka na koje možete naići u zadacima i pomenut je u lekciji je poprečni ili paralelni presek i nije ništa drugo nego krug podudaran krugu u osnovi i njegovu površinu računamo po formuli:
ovde je B, naravno, oznaka za površinu baze.
Osim što imate za domaći da sami izvučete iz lekcije najbitnije i nacrtate nastajanje valjka rotacijom, imate i da uradite koji zadačić iz vaše školske zbirke sa strane 117. Zadaci su: 3, 4, 5, i 7.




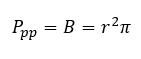


Comments
Post a Comment