Proizvod dva razlomka
Primer
Data je duž |AB| = 8 cm. Kolika je dužina duži AC koja čini: a) 1/4 duži AB; b) 3/4 duži AB?
Data je duž |AB| = 8 cm. Kolika je dužina duži AC koja čini: a) 1/4 duži AB; b) 3/4 duži AB?
Kada smo tek počeli da učimo razlomke, radili smo i određivanje dela neke veličine kada je taj deo predstavljen razlomkom, pa tako možemo da uradimo i ovaj primer.
a) |AC| = (8 : 4) ∙ 1 = 2 cm b) |AC| = (8 : 4) ∙ 3 = 2 ∙ 3 = 6 cm
Na jednom od prošlih časova, kada smo učili množenje decimalnih brojeva, utvrdili smo da deo od nečega predstavljamo množenjem odgovarajućeg razlomka koji predstavlja deo i date celine (za domaći ste imali da izračunate 0,9 od 3,25 i to ste računali kao 0,9 ∙ 3,25 = 2,925) pa bismo sigurno tako mogli da uradimo i ovaj zadatak.
Zaključujemo da će biti:
a) |AC| = 1/4 ∙ |AB| = 1/4 ∙ 8 = 2 cm
b) |AC| = 3/4 ∙ |AB| = 3/4 ∙ 8 = 6 cm
Ovo sigurno mora biti tačno jer se slaže sa svim onim što smo prethodno naučili a sada ćemo otkriti i zašto je to tako i kako zaista onda množimo dva razlomka.
Primer
Nacrtajte kvadrat i zamislimo da je njegova stranica dužine 1m. Njegova površina je onda 1m ∙ 1m = 1m². Kolika će biti površina pravougaonika čija je jedna stranica dužine 2/5 stranice ovog kvadrata, a druga 3/4 stranice ovog kvadrata?
Njegove stranice bi onda bile 2/5 m i 3/4 m i trebali bismo da ih pomnožimo da bismo odredili površinu pravougaonika. Taj problem ćemo nacrtati i odrediti površinu pravougaonika kao deo površine kvadrata.
Na prvom kvadratu sam označila šta bi bila dužina prve stranice tako što sam podelila kvadrat na petine, označila blago dve, i obojila plavim dužinu stranice novog pravougaonika kojeg ćemo dobiti. Isto to sam uradila i označavajući 3/4 stranice na drugoj sličici. Na trećoj je kvadrat podeljen na 4 ∙ 5 = 20 manjih polja kako bismo lakše nacrtali naš pravougaonik čije su stranice 2/5 i 3/4 i njegova površina zahvata 6 malih polja od ukupno 20, što znači da je njegova površina 6/20. Ovde se sasvim lepo vidi i kako množimo dva razlomka.
Proizvod dva razlomka je razlomak čiji je brojilac proizvod brojilaca ta dva razlomka, a imenilac proizvod imenilaca ta dva razlomka.
Ili kako bismo mi to jednostavnije rekli, razlomke ćemo pomnožiti tako što im pomnožimo brojioce i pomnožimo imenioce. Naravno, kasnije taj razlomak skratimo ako može.
Možete pokušati još par ovakvih primera, da se igrate sa ovim pravougaonicima i površinama u zadačiću na ovom linku, a dalje ćemo videti po jedan primer kako množimo razlomke i cele brojeve, mešovite...
Dakle, kada množimo razlomak sa celim brojem, setimo se da svaki ceo broj u imeniocu ima 1, dopišemo ga i množimo kao i svaki drugi razlomak.
Kada množimo mešovite brojeve, obavezno ih pretvaramo prvo u razlomke.
Postoji jedna zanimljiva stvar koju možemo da radimo kod množenja i koja nam olakšava računanje, pogotovo ako su veći brojevi u pitanju. Setimo se kako smo skraćivali razlomke kada smo imali proizvode u brojiocu i u imeniocu, kako smo birali koje nam je brojeve najpogodnije da delimo istim i da na taj način skratimo brojeve i učinimo kasnije računanje jednostavnijim. To isto možemo raditi i prilikom množenja razlomaka i taj postupak zovemo unakrsnim skraćivanjem:
Postupno unakrsno skraćivanje možete još jednom pogledati na ovom linku. Povlačenjem klizača sa strane prikazuje vam se polako postupak.
Uradićemo još dva zadačića iz vaše zbirke.
1.
U primeru pod b) i v) je korišćeno unakrsno skraćivanje u drugom koraku.
2.
Domaći zadatak: šarena zbirka za domaće zadatke, strana 100.
Ne morate odmah sve ali gledajte da malo provežbate.





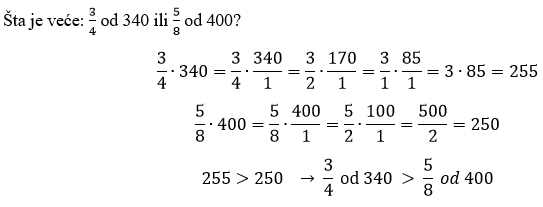


Comments
Post a Comment