Rastojanje između dve tačke i sredina duži - vežbe
Današnji zadatak nam je da utvrdimo šta smo naučili, primenimo malo to znanje i da naučimo kako možemo da izračunamo površinu trougla čija su temena zadata koordinatama u koordinatnom sistemu.
1. Odredi površinu trougla ABC ako su njegova temena:
a) A(-4, -4), B(-4,1), C(-2,1);
b) A(2, -1), B(2, -7), C(4, -4).
Treba da odredimo površinu trougla ako su nam zadate koordinate njegovih temena. To možemo uraditi na dva načina: ucrtavanjem tačaka u KS ili preko jedne malo duže formule ali zabavne 😁
Uradićemo dva primera na oba načina. Prvi način sa crtanjem nije uvek pogodan jer ne mora da znači da ćete dobiti trougao gde lako prepoznajete osnovicu i visinu za računanje površine (mada su ovde obično namešteni brojevi da to tako bude). Dok drugi način uvek "radi posao", možete i sami nacrtati bilo kakav neobičan trougao u svesci i odrediti koordinate temena i pomoću ove formule uvek lako računate površinu. Zato je ova oblast super, olakšava rešavanje nekih problema. Manje priče, krećemo sa radom.
a) A(-4, -4), B(-4,1), C(-2,1)
Nemojte da vas ova formula plaši, nije toliko teška za pamćenje, olakšaću vam. Nadam se da primećujemo da u apsolutnim zagradama imate tri slična, skoro ista sabirka: uvek vam x koordinata množi razliku y koordinata, jedino treba zapamtiti od kojih tačaka. Redosled je lak za pamćenje.
Prvo složite indekse redom, A B C, zatim prvo slovo šaljete na kraj pa nastaje B C A i na kraju još jednom prvo slovo šaljete na kraj i nastaje C A B. Nije toliko teško, zar ne? Probajte par puta da je raspišete, brzo se nauči. Naravno, apsolutna zagrada je tu da ne dozvoli negativnu površinu a i na polovine smo navikli u formulama za površinu trougla, zar ne? Idemo na naredni primer, pokušajte sami, ja ću vam uraditi opet na oba načina.
b) A(2, -1), B(2, -7), C(4, -4)
2. Rastojanje tačke M od koordinatnog početka je 13. Odredi apscisu tačke M ako znaš da joj je ordinata 12.
Zadato je rastojanje tačke M od koordinatnog početka O(0, 0), ⏐MO⏐ = 13 i znamo da je njena apscisa 12 a traži se ordinata. Setimo se da je apscisa naziv za x koordinatu (ali i osu), a ordinata je y koordinata. Treba nam formula za rastojanje tačke od O (0, 0):
U ovom zadatku smo dobili dva rešenja, tačka M može imati koordinate (12, 5) ili (12, -5). Zašto? Vidimo sa slike da obe tačke zadovoljavaju uslove zadatka, zaista su obe na rastojanju 13 od O i imaju x koordinatu 12. Moramo imati u vidu da koordinate mogu biti negativne i zato prilikom rešavanja kvadratne jednačine y² = 25 (za koju znamo da uvek ima dva rešenja) ne smemo zaboraviti ni da se kvadriranjem broja -5 isto dobija 25.
3. Ako su tačke A(-2, 2) i B(1, 2) temena kvadrata ABCD, odredi koordinate tačaka C i D.
Treba ucrtati tačke u KS i formirati kvadrat. Na koliko načina to možemo uraditi?
Za ovako fiksiranu duž AB postoje dva rešenja:
4. Dijagonala kvadrata ABCD je duž AC, zadata tačkama A(-3, 4), C(3, 4). Odredi:
a) koordinate druga dva temena kvadrata; b) O i P kvadrata.
5. Izračunaj obim i površinu četvorougla čija su temena A(1, 0), B(8, 0), C(4, 3), D(1, 3).
Ja ću nacrtati, vi odgovorite na ostale zahteve zadatka.
6. Zadate su tačke A(-2, 5), B(4, -9), C(-11, 0), D(-3, 8). Odredi koordinate središta duži AB i duži CD a zatim izračunaj rastojanje tih središta.
Odredimo prvo središta tih duži.
Domaći zadatak:
1. Tačka M je na rastojanju 17 od koordinatnog početka. Odredi ordinatu tačke M ako znaš da joj je apscisa -8.
2. Zadate su tačke A(-10, 7), B(16, 15), C(-8, -15), D(0, -11). Odredi koordinate središta duži AB i duži CD a zatim izračunaj rastojanje tih središta.






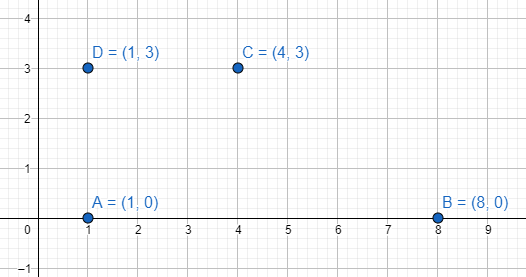




Comments
Post a Comment