Direktno proporcionalne veličine

Obavezno odgledajte video lekciju koja se tiče naše današnje teme a mi ćemo još jednom sve ponoviti, istaći najbitnije i uraditi primere iz vaše zbirke.

Prošli čas smo videli kako neke veličine zavise jedna od druge, kako tu zavisnost možemo da zapišemo i kako je grafički predstavljamo. Setimo se primera sa masom i zapreminom. Podatke za naše tri kocke smo prikazali u tabeli.

Ako bi nas zanimao odnos mase i zapremine, onda bismo ispitivali količnik mase i zapremine za sve tri kolone. Šta zaključujemo?

Količnik je uvek isti, 2,5. Možemo da kažemo da je odnos 2,5 prema 1 ili da pretvorimo to u razlomak i kažemo 5 prema 2 (5 : 2, ili 5/2). Naravno, da sam tražila odnos zapremine i mase, odgovor bi bio 2 : 5 jer uvek vodim računa koju veličinu prvo navodim pa tako i delim. Za ove veličine koje imaju količnik koji se ne menja kažemo da su direktno proporcionalne tj. ako posmatram veličine y i x:

Veličina y je direktno proporcionalna veličini x ako je odnos y/x svih njihovih odgovarajućih vrednosti uvek isti (konstantan) broj različit od nule.

Taj konstantan broj, količnik, označavam sa k i nazivam ga koeficijentom proporcionalnosti.

Direktnu proporcionalnost mogu da zapišem i na sledeći način, izražavanjem zavisne veličine y:

Dakle, u zadacima koristimo jedan od ova dva oblika.

U našem primeru je koeficijent proporcionalnosti k = 2,5.

Uradićemo par zadataka iz vaše zbirke sa strane 105. i usput objašnjavati još neke bitne stvari.

1. Veličine x i y su direktno proporcionale. Ako je koeficijent proporcionalnosti k = 3, popuni datu tabelu:

Kako nam je zadat koeficijent k = 3 a traži nam se y, koristićemo oblik y = k ∙ x, tj. y = 3 ∙ x. Jednostavnim računom dobijamo:

Primetićemo da u tabeli imamo kolonu sa vrednostima x = 0 i odgovarajućim y = 0. To će uvek biti tako kod direktne proporcionalnosti jer je 0 = k ∙ 0. Ove vrednosti nikad ne koristimo za izračunavanje k u k = y/x jer znamo da deljenje nulom nije definisano ali ipak znamo da ove vrednosti uvek imamo u tabeli za direktnu proporcionalnost.

2. Veličine x i y date tabelom su direktno proporcionalne. Odredimo koeficijent proporcionalnosti.

Koeficijent proporcionalnosti određujemo iz k = y/x računajući količnik za svaku kolonu (sem prve, nju preskačemo zbog nula, samo konstatujemo da je ona u redu) i proveravajući da li je količnik svuda isti.

k = 2/1 = 2,   k = 4/2 = 2,   k = 10/5 = 2,  k = 20/10 = 2 →  zaključujemo da je k = 2

3. Ispitajmo da li su veličine x i y date tabelom direktno proporcionalne.

Proverimo količnike y/x:

k = 3/6 = 1/2,   k = 2/4 = 1/2,  k = 1/2 = 1/2    iz ovoga vidimo da bi trebalo da je k = 1/2.

Proverimo kolonu sa nulama: y = k ∙ x   dobijamo    1 = 1/2 ∙ 0  što je nemoguće a i znamo da kolona mora biti x = 0 i y = 0, prema tome, pošto se ova kolona ne slaže, veličine NISU direktno proporcionalne. Naravno, dovoljna je samo jedna kolona da se ne slaže pa svaki put moramo proveriti svaku.

4. Ako su x i y direktno proporcionalne veličine, odredi koeficijent proporcionalnosti, popuni tabelu, zapiši zavisnost veličina formulom i nacrtaj njen grafik:

U ovom zadatku imamo dosta zahteva, sve ćemo preći i još jednom ponoviti. Zadatak kaže da jesu x i y direktno proporcionalne ali moramo da otkrijemo koliko je k. To ćemo naravno iz jedinog potpunog podatka koji je treća kolona jer tu imate i vrednost za x i vrednost za y.

x = 2,  y = 6   → k = y/x = 6/2 = 3, dakle, koeficijent proporcionalnosti je 3, pa je onda

zavisnost y od x iskazana formulom: y = 3 ∙ x

I sada možemo da popunimo tabelu računajući x ili y koje nedostaje uz pomoć formule iznad:

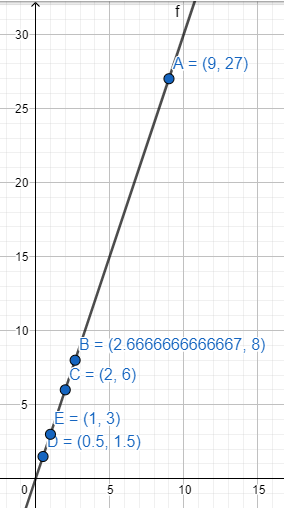
Ostalo nam je još da nacrtamo grafik zavisnosti ove dve veličine. Kao i prošlog časa, svaka kolona će nam dati po jednu tačku sa odgovarajućim koordinatama koje ćemo ucrtati u KS:

A(9, 27), B(8/3, 8), C(2, 6), D(1/2, 3/2), E(1, 3)

Primećujemo da i tačka (0, 0) pripada grafiku zavisnosti što smo već rekli da mora da važi za direktno proporcionalne veličine. Isto tako:

Odnos koordinata svake tačke neke prave koja sadrži koordinatni početak je isti.

Taj odnos je kod nas k = 3 i on nam baš pokazuje nagib pod kojim će biti ova prava. Primetite kako se lepo vidi da i tačka (5, 15) isto pripada ovom grafiku jer je i za nju k = 15/5 = 3.

5. Nacrtaj grafik zavisnosti direktne proporcionalnosti y = 2x za x ≥ 0.

Pošto nemamo zadate vrednosti, možemo ih sami birati, tj. biramo vrednosti za nezavisnu promenljivu x, izračunavamo y koordinate i date tačke ucrtavamo u KS.

Ja biram ovako npr, naravno, poštujući uslov da je x nenegativno:

6. Odredi koeficijent direktne proporcionalnosti veličina čijem grafiku pripada tačka A(2, 10).

Već smo rekli da količnik koordinata svake tačke koja pripada grafiku direktne proporcionalnosti mora biti jednak koeficijentu k za datu direktnu proporcionalnost.

k = y/x,    k = 10/2 = 5

Prema tome, ova direktna proporcionalnost je y = 5x, njeno k = 5, i tačka A se nalazi na njenom grafiku.

7. Neko telo se kreće ravnomernom brzinom od 12 km/h. Izrazi zavisnost pređenog puta od vremena i nacrtaj grafik te zavisnosti.

Znamo da je v = s/t. Zadatak kaže da je v = 12 km/h, prema tome: 12 = s/t. Kako se traži zavisnost puta od vremena, mi naše s treba da izrazimo. Pređeni put se računa kao proizvod v i t tj.

12 = s/t   →   s = 12 ∙ t

Zaključujemo da su pređeni put i vreme direktno proporcionalne veličine (povećavanjem vremena, povećava se i put koji smo prešli za ovu, stalnu brzinu od 12 km/h) i da je koeficijent direktne proporcionalnosti ovde 12.

Grafik zavisnosti:

Domaći zadatak: školska zbirka, strana 105, zadaci: 2. b), 3. a), 4. b), 5. b), đ), 6. b), v).