Svojstva množenja razlomaka
Još u prvom polugodištu smo ponavljali prirodne brojeve i osobine koje važe za njihovo sabiranje i množenje. Ništa se mnogo neće promeniti ni kod razlomaka. Navodićemo jednu po jednu osobinu i ponavljati, videti gde, kako i zašto ih koristimo na primerima. Ova lekcija je u vašim udžbenicima na strani 172.
- komutativnost množenja (zamena mesta)
Primer
a)
Računanjem leve i desne strane jednakosti vidimo da zaista nije bitno kojim redom navodimo činioce.
b) Da bismo pokazali gde i kako to koristimo, uradićemo naredni primer
4 ∙ 0,00987 ∙ 25 = ? Primer je malo teži za računanje ako ne primetimo da možemo da računamo sa "okruglim" brojevima pa da nam bude mnogo jednostavnije. Šta treba da primetimo? Treba da primetimo da zamenom mesta drugom i trećem činiocu olakšavamo sebi jer znamo da je 4 ∙ 25 = 100:
4 ∙ 0,00987 ∙ 25 = 4 ∙ 25 ∙ 0,00987 = 100 ∙ 0,00987 = 0,987
- asocijativnost (združivanje)
Primer Ako treba da pomnožimo tri broja, uvek možemo da biramo koja dva ćemo prvo pomnožiti, pogotovo jer znamo da možemo da korisitmo unakrsno skraćivanje pa nije loše prvo skratiti naešto, ako može, da bismo računali sa manjim brojevima:
a)
Broj 1 je neutralni element za množenje, jer kao činilac ne utiče na vrednost proizvoda.
Bilo koji broj pomnožen nulom daje proizvod 0. Nulom se ne može deliti!
Za bilo koji razlomak r važi:
b) Komutativnost i asocijativnost često koristimo zajedno u nekim zadacima radi lakšeg računanja:
Iste osobine koje su važile za računanje sa 0 i 1 kod prirodnih brojeva, važe i dalje.
Za bilo koji razlomak r važi:
- distributivnost množenja
Distributivnost množenja je osobina koja nam govori kako razlomak množi neki zbir (videćemo da može da se koristi i kada je razlika u zagradi). Razlomak množi zbir tako što množi oba broja iz zagrade:
Primer
Mi ovu osobinu ipak češće koristimo kada želimo da skratimo proces računanja, tj. formulu koristimo u drugom smeru, tako što "izvlačimo" isti činilac koji uočimo ispred zagrade i na taj način imamo manje operacija da izvršimo:
Primer
Primetimo kako sam i u zagradi uočila dva broja koja će mi dati jedno celo pa sam i na taj način brže izračunala zbir u zagradi.
Primer U ovom primeru ćemo na dva različita načina izračunati vrednost izraza i pokazati da distributivnost važi i za razliku.
Gde smo brže sračunali? 😊
Domaći zadatak: šarena zbirka za domaće zadatke, strana 104. i 2, 4. i 5. zadatak koji su nam ostali sa strane 101.
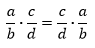


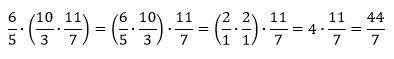








Comments
Post a Comment