Složenije jednačine i nejednačine
Obavezno odgledajte lekciju Složenije jednačine ako ste je propustili, poslušajte kako se rešavaju, mi ćemo ponoviti i pokazati na par primera a takvo rešavanje primenjujemo i kod nejednačina.
Dakle, današnji zadatak nam je da naučimo kako da rešavamo jednačine i nejednačine sa više operacija.
Primer Izračunaj vrednost izraza: 2,6 ∙ 1,07 - 0,3.
Ovaj izraz sadrži u sebi dve operacije: množenje i oduzimanje. Znamo da prednost ima množenje, pa prvo računamo proizvod:
2,6 ∙ 1,07 - 0,3 = 2,782 - 0,3 = 2,482 107 ∙ 26
642
+ 214
2782
Primer Reši jednačinu: 2,6 ∙ x - 0,3 = 8,15
Primećujemo da leva strana jednačine podseća na izraz koji smo računali i da isto ima opercije množenja i oduzimanja. Kako ćemo je rešiti? Pomoći će nam prethodni primer jer nam on govori šta smo prvo računali. Prilikom rešavanja jednačine sa više operacija ako zamislimo da izračunavamo vrednost izraza i obratimo pažnju na operaciju koja ima prednost, upravo taj deo izraza posmatram kao jedan veliki nepoznati član jednačine, jedno veliko x.
U našem primeru kao jedan veliki X zamišljam 2,6 ∙ x jer bih taj deo izračunala prvo da je ovo bio izraz i sada mi je 2,6 ∙ x nepoznati umanjenik:
2,6 ∙ x - 0,3 = 8,15
↱ nepoznati umanjenik
2,6 ∙ x = 8,15 + 0,3
2,6 ∙ x = 8,45
Kada smo odredili nepoznati umanjenik, mi i dalje nismo otkrili koliko je x. Ovo su jednačine u kojima se u stvari kriju dve ili čak više jednačina u zavisnosti od toga koliko imamo operacija u samoj jednačini i moramo je rešiti do kraja dok ne otkrijemo koliko je baš x.
2,6 ∙ x = 8,45
↖ nepoznati činilac
x = 8,45 : 2,6
x = 845 : 260
x = 3,25
Isti je postupak i prilikom rešavanja složenije nejednačine.
Primer Reši nejednačinu: (x + 1/2) : 3,2 < 2 cela 1/20
1/2 = 0,5 2 cela 1/20 = 2 cela 5/100 = 2,05
Prednost ima zagrada, zato je ona nepoznati deljenik:
(x + 0,5) : 3,2 < 2,05
x + 0,5 < 2,05 ∙ 3,2
205 ∙ 32
410
+ 615
6560 ⇒ 2,05 ∙ 3,2 = 6,560 = 6,56
x + 0,5 < 6,56
x < 6,56 - 0,5
x < 6,06
1. Reši jednačinu:
Ovde se obavezno sve pretvara u razlomke jer devetine i dvanaestine sadrže u sebi 3 i iz tog razloga ne možemo imenioce da proširimo do dekadne jedinice da bismo kasnije pretvarali u decimalni broj.
Ovde se obavezno sve pretvara u razlomke jer devetine i dvanaestine sadrže u sebi 3 i iz tog razloga ne možemo imenioce da proširimo do dekadne jedinice da bismo kasnije pretvarali u decimalni broj.
2. (školska zbirka, strana 185, zadatak 172.) Pročitajte zadatak, pokušajte da sastavite i rešite jednačinu. Primetićemo da u ovom slučaju imamo zagradu u kojoj su samo brojevi povezani operacijom oduzimanja, kao i na desnoj strani jednačine operacija deljenja. Ovo, naravno, možemo izračunati i uprostiti izgled naše jednačine da bismo je rešili.
3. (strana 184, zadatak 170. b)) U ovom primeru vidimo da neki proizvod treba da bude jednak nuli. Kada nam se dešava da pomnožimo dva broja i dobijemo rezultat 0? Proizvod je jednak nuli ako je bar jedan činilac nula. Ovde je prvi činilac 2,7 i sigurno nije jednak nuli pa ovu jednačinu možemo da uprostimo tako što zaključujemo da drugi činilac mora biti nula i tu jednačinu rešavamo:
Pokazaćemo još par primera sa složenijim nejednačinama iz vaše zbirke sa strane 189.
4. a) (202. đ))
b) (202. e))
Obratimo pažnju na menjanje znaka nejednakosti u suprotan jer je nepoznat bio umanjilac. Ne smemo zaboravljati na to.
Pokazaćemo za kraj i jednu malo dužu nejednačinu.
5. (204. b))
Domaći zadatak: šarena zbirka za domaće zadatke, strana 116. zadatak 3. i sa strane 114. koliko uspete da uradite ali minimum 1. zadatak.
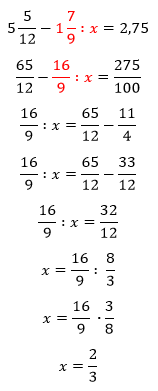







Comments
Post a Comment