Površina i zapremina lopte - vežbe

19./137. Lopta prečnika 4√3 cm i ravnostrana kupa imaju jednake površine. Za koliko se razlikuju njihove zapremine?

2r₁ = 4√3   ⇒   r₁ = 2√3 cm       P₁ - površina lopte,  P₂ - površina kupe
lopta
V₁ = 4 ∙ r₁³𝜋/3
V₁ = 4 ∙ (2√3)³𝜋/3 = 4 ∙ 8 ∙ 3√3𝜋/3 = 32√3𝜋 cm³
P₁ = 4 ∙ r₁²𝜋
P₁ = 4 ∙ (2√3)²𝜋 = 4 ∙ 4 ∙ 3𝜋 = 48𝜋 cm²
P₁ = P₂
kupa
P₂ = r₂²𝜋 + r₂∙𝜋∙s, a kako je kupa ravnostrana:  2r₂ = s,
                            osni presek je jednakostranični trougao, H₂ = 2r₂√3/2 = r₂√3
P₂ =  r₂²𝜋 + r₂∙𝜋∙2r₂ = 3r₂²𝜋
P₁ = P₂
3r₂²𝜋 = 48𝜋 cm²     /:3𝜋
r₂² = 16   ⇒    r₂ = 4 cm,     H₂ = 4√3 cm
V₂ = r₂²𝜋 ∙ H₂/3
V₂ = 16𝜋 ∙ 4√3/3 = 64√3𝜋/3 cm³
V₁ - V₂ = 32√3𝜋 - 64√3𝜋/3 = (32 - 64/3)∙√3𝜋 = 32√3𝜋/3 cm³

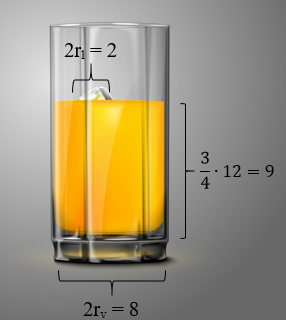
23. U čašu oblika valjka prečnika 8 cm ubacili smo 3 kuglice leda prečnika 2 cm. Koliko soka možemo sipati u čašu ako je visina čaše 12 cm, a želimo da napunimo 3/4 čaše?

Ako se zapremina valjka računa: V = r²𝜋 ∙ H
a mi moramo da napunimo čašu do 3/4 visine,
zapremina sadržine čaše mora biti:

Vukupno = 4²𝜋 ∙ 9 = 16 ∙ 9𝜋 = 144𝜋 cm³

gde je rv = 4 cm

Zapremina 3 kuglice leda  (rl = 1 cm):

Vleda = 3 ∙ 4/3 ∙ rl³𝜋 = 4 ∙ rl³𝜋 = 4𝜋 cm³

Zapremina soka koji treba sipati je onda:

Vsoka = Vukupno - Vleda = 140𝜋 cm³

Domaći zadatak: zadaci 22. i 25. sa 137. strane vaše školske zbirke koji nisu toliko teški, a zatim počnite da prelazite zadatke iz zbirke za završni iz obrtnih tela koje mi ne morate slati, samo ako ima pitanja. Navešću brojeve zadataka iz prošlogodišnje zbirke:

osnovni nivo: 107. - 111.

srednji nivo: 268. - 275.

napredni nivo: 406. - 410.