Sfera i lopta

Koja je razlika između kružnice i kruga? Kružnicu čine sve tačke koje su na podjednakoj udaljenosti od jedne fiksirane tačke, centra kružnice. Dakle, kružnica je samo kružna linija, dok krug čine i kružnica i sve tačke unutrašnje oblasti koju ograničava data kružnica. Slično je i sa pojmovima sfere i lopte.

Sfera je skup svih tačaka prostora podjednako udaljenih od jedne fiksirane tačke, centra sfere.

Poluprečnik sfere r je rastojanje bilo koje tačke sfere od centra sfere.

Lopta je oblo telo ograničeno sferom.

Lopta nastaje obrtanjem kruga oko bilo kog njegovog prečnika.

Presek neke ravni i lopte može biti: 

                   1) prazan skup  𝛼 ∩ L = ∅

                   2) tačka    𝛾 ∩ L = {T}

                   3) krug     𝛽 ∩ L = K

U sva tri slučaja je različito rastojanje ravni od centra lopte O. Ako to rastojanje označimo slovom d, u prvom slučaju je ono veće od r (d > r), u drugom jednako sa r (d = r), a u trećem manje od r (d < r). Ako je presek tačka, tada ravan dodiruje loptu i ta ravan se onda naziva tangentna ravan.

Nama je najzanimljiviji slučaj u kojem je d < r, tj. slučaj u kojem ravan seče loptu. Ako ravan koja seče loptu sadrži njen centar, tada je presek krug sa najvećom površinom kojeg nazivamo veliki loptin krug. U suprotnom je presek mali loptin krug.

Sve ovo a i malo više možete još jednom čuti u narednom klipu.

Ako sa r označimo poluprečnik lopte, površinu velikog loptinog kruga računamo:

Pvk = r²𝜋

dok njegov obim računamo:

Ovk = 2r𝜋

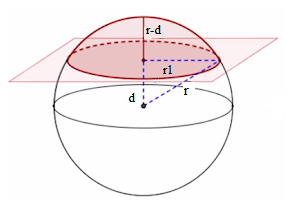
Pozabavimo se sad slučajem kada presečna ravan ne prolazi kroz centar lopte. Tada je rastojanje ravni od centra O, manje od poluprečnika d < r, u preseku je mali krug sa poluprečnikom r₁ i sa slike možemo da uočimo pravougli trougao kojeg tad čine r, r₁ i d i da sastavimo vezu između njih upotrebom Pitagorine teoreme:

r² = d² + r₁²

Primer Loptu poluprečnika 17 cm preseca ravan na rastojanju 15 cm od centra lopte. Izračunaj površinu preseka ravni i lopte.

Površina preseka ravni i lopte je površina malog kruga: Pmk = r₁²𝜋.

Zadatak nam je da prvo odredimo r₁.

r = 17 cm,   d = 15 cm,  Pmk = ?

r² = d² + r₁²

17² = 15² + r₁²         ⇒     r₁² = 289 - 225 = 64      ⇒   r₁ = 8 cm,     Pmk = 8²𝜋 = 64𝜋 cm²

Primer (8./135.)  r = 10 cm,   d = r/2,  Pvk : Pmk = ? 

d = 5 cm

r² = d² + r₁²

r₁² = 10² - 5² = 100 - 25 = 75  ⇒   r₁ = 5√3 cm

Pvk = 100𝜋,      Pmk = 75𝜋          Pvk : Pmk = 100𝜋 : 75𝜋 = 4 : 3

Domaći zadatak: školska zbirka, strana 135. zadaci: 4. - 7.