Razmera
Primeri razmere:
Za razmeru ste možda čuli na časovima geografije gde ste spominjali razmeru na karti koja predstavlja odnos tj. količnik dužina na karti i u stvarnosti. Pogledajmo primere na slici.
Na poslednjem primeru je karta rađena u razmeri 1 : 25000 (čita se 1 prema 25000) što nam govori da 1 cm na karti predstavlja 25000 cm u prirodi ili da 3 cm na karti sigurno onda predstavljaju 75000 cm u prirodi (3 ∙ 25000). I vrlo je važno da ispratimo da se prvi broj uvek odnosi na dužinu na karti a drugi na dužinu u stvarnosti, što i nije ništa čudno s obzirom na to da je drugi broj veći pa nam je to prirodno.
Za razmeru ste mogli čuti još i u receptima gde možda nemate tačne mere sastojaka ali je bitan njihov odnos pa sami birate koliko ćete upotrebiti na osnovu onog što imate. Ako recept kaže "pirinač naliti vodom u razmeri 1 : 3", šta to znači? To znači da na jednu meru pirinča ide tri mere vode tj. ja mogu sipati 1 šolju pirinča i 3 šolje vode ili čak i 1 kantu pirinča i 3 kante vode. Zanimljivo je još i korisno da znamo da je isto i kad bih sipala 2 šolje pirinča i onda mi treba 6 šolja vode. Da li se slažemo? Zapišite sebi ove primere. Nadam se da ste razumeli čime ćemo se baviti i šta sam ja to ovde radila sa brojevima kad smo rekli da su neke stvari iste, a sada ćemo lepo definisati sve i dati pravila za računanje i korišćenje ovih pojmova.
Razmera je količnik dve veličine.
y : x = k
↖ ↗ ↖
članovi vrednost
razmere razmere
Primer Ako su razlomci u razmeri, da bismo je pojednostavili, što uvek gledamo da uradimo, možemo ih zameniti celim brojevima tako što ćemo izračunati količnik tih brojeva:
ili možemo iskoristiti
Osnovno svojstvo razmere:
koje kaže da ako oba člana razmere pomnožim (ili podelim) istim brojem, razmera se neće promeniti.
Kada su razlomci u pitanju, uvek se množi sa NZS za imenioce, u našem primeru sa 15:
Primer Posmatrajmo još jednom primer sa pirinčem i vodom koji se odnose kao 1 : 3.
a) Koliko mi treba vode ako imam 400 g pirinča?
b) Koliko mi treba pirinča za jednu i po šerpu vode?
a) 1 : 3 = (1 ∙ 400) : (3 ∙ 400) = 400 : 1200 → treba 1200 g vode
b) 1 : 3 = (1 : 2) : (3 : 2) = 0,5 : 1,5 → treba pola šerpe pirinča
Kada kažemo da su pirinač i voda u razmeri 1 : 3 to znači da se 1 odnosi na pirinač a broj 3 na vodu, uvek tim redom. Razmera vode i pirinča bi u ovom slučaju bila 3 : 1 jer sam im i nazive navela obrnutim redosledom.
Šta još možemo zanimljivo da zaključimo na ovom primeru?
Ova razmera nam govori da uvek vode ima tri puta više od pirinča jer se na nju odnosi broj 3 a na pirinač broj 1.
Primer Razmera se obično koristi kada se prave neki rastvori ili kad se koriste razni deterdženti pa se navede u uputstvu da "na 50 ml deterdženta sipate 5 l vode". Koja je ovde razmera u pitanju? (1l = 1000 ml).
50 ml : 5 l = 50 : 5000 = 10 : 1000 = 1 : 100
Primer Uprostite razmere (nek im članovi budu prirodni, uzajamno prosti brojevi):
a) 0,12 : 0,036 b) (8 celih 3/4) : (4 cela 1/12)
a) 0,12 : 0,036 = (0,12 ∙ 1000) : (0,036 ∙ 1000) = 120 : 36 = (120 : 12) : (36 : 12) = 10 : 3
b) 35/4 : 49/12 = (35/4 : 7) : (49/12 : 7) = 5/4 : 7/12 = (5/4 ∙ 12) : (7/12 ∙ 12) = 15 : 7
Domaći zadatak: šarena zbirka za domaće zadatke, strana 119.



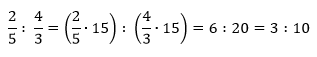


Comments
Post a Comment