Razmera i proporcija
Primeri razmere:
Za razmeru ste čuli na časovima geografije gde ste spominjali razmeru na karti koja predstavlja odnos tj. količnik dužina na karti i u stvarnosti. Pogledajmo primere na slici.
Na poslednjem primeru je karta rađena u razmeri 1 : 25000 (čita se 1 prema 25000) što nam govori da 1 cm na karti predstavlja 25000 cm u prirodi ili da 3 cm na karti sigurno onda predstavljaju 75000 cm u prirodi (3 ∙ 25000). I vrlo je važno da ispratimo da se prvi broj uvek odnosi na dužinu na karti a drugi na dužinu u stvarnosti, što i nije ništa čudno s obzirom na to da je drugi broj veći pa nam je to prirodno.
Za razmeru ste mogli čuti još i u receptima gde možda nemate tačne mere sastojaka ali je bitan njihov odnos pa sami birate koliko ćete upotrebiti na osnovu onog što imate. Ako recept kaže "pirinač naliti vodom u razmeri 1 : 3", šta to znači? To znači da na jednu meru pirinča ide tri mere vode tj. ja mogu sipati 1 šolju pirinča i 3 šolje vode ili čak i 1 kantu pirinča i 3 kante vode. Zanimljivo je još i korisno da znamo da je isto i kad bih sipala 2 šolje pirinča i onda mi treba 6 šolja vode. Da li se slažemo? Zapišite sebi ove primere. Nadam se da ste razumeli čime ćemo se baviti i šta sam ja to ovde radila sa brojevima kad smo rekli da su neke stvari iste, a sada ćemo lepo definisati sve i dati pravila za računanje i korišćenje ovih pojmova.
Razmera je količnik dve veličine.
y : x = k
↖ ↗ ↖
članovi vrednost
razmere razmere
Primer Ako su razlomci u razmeri, da bismo je pojednostavili, što uvek gledamo da uradimo, možemo ih zameniti celim brojevima tako što ćemo izračunati količnik tih brojeva:
ili možemo iskoristiti
Osnovno svojstvo razmere:
koje kaže da ako oba člana razmere pomnožim (ili podelim) istim brojem, razmera se neće promeniti.
Kada su razlomci u pitanju, uvek se množi sa NZS za imenioce, u našem primeru sa 15:
Primer Posmatrajmo još jednom primer sa pirinčem i vodom koji se odnose kao 1 : 3.
a) Koliko mi treba vode ako imam 400 g pirinča?
b) Koliko mi treba pirinča za jednu i po šerpu vode?
a) 1 : 3 = (1 ∙ 400) : (3 ∙ 400) = 400 : 1200 → treba 1200 g vode
b) 1 : 3 = (1 : 2) : (3 : 2) = 0,5 : 1,5 → treba pola šerpe pirinča
Primer Razmera se obično koristi kada se prave neki rastvori ili kad se koriste razni deterdženti pa se navede u uputstvu da "na 50 ml deterdženta sipate 5 l vode". Koja je ovde razmera u pitanju? (1l = 1000 ml).
50 ml : 5 l = 50 : 5000 = 10 : 1000 = 1 : 100
Proporcija je jednakost dve razmere:
a i d su spoljašnji članovi, b i c su untrašnji članovi
Kada su dve razmere jednake? Pa kada je vrednost razmere isti broj.
Primer Brojevi 13 i 39 se odnose isto kao i brojevi -18 i -54. Zašto?
Odnos brojeva 13 i 39, tj. njihova razmera je 13 : 39 = (13 : 13) : (39 : 13) = 1 : 3 = 1/3
a odnos brojeva -18 i -54 je -18 : (-54) = (-18 : (-18)) : (-54 : (-18)) = 1 : 3 = 1/3.
Kako su im vrednosti razmere jednake, oni čine proporciju:
Kada su dve razmere jednake? Pa kada je vrednost razmere isti broj.
Primer Brojevi 13 i 39 se odnose isto kao i brojevi -18 i -54. Zašto?
Odnos brojeva 13 i 39, tj. njihova razmera je 13 : 39 = (13 : 13) : (39 : 13) = 1 : 3 = 1/3
a odnos brojeva -18 i -54 je -18 : (-54) = (-18 : (-18)) : (-54 : (-18)) = 1 : 3 = 1/3.
Kako su im vrednosti razmere jednake, oni čine proporciju:
13 : 39 = -18 : (-54)
gde su 13, 39, -18 i -54 redom prvi, drugi, treći i četvrti član proporcije a 13 i -54 spoljašnji članovi (jer su sa krajeva), a 39 i -18 unutrašnji članovi proporcije.
Ako se setimo, kada imate jednakost dva razlomka, tada možemo da zaključimo sledeće:
to smo zvali unakrsno množenje.
Primer
Ono nam pomaže da rešimo proporciju tj. daje nam njenu osnovnu osobinu na osnovu koje je rešavamo.
Osnovno svojstvo proporcije:
Množenjem spoljašnjih članova proporcije dobijam isti rezultat kao i množenjem unutrašnjih članova proporcije.
Primer Proveri da li su tačne proporcije:
a) 3 : 2 = 9 : 6
⇒ 3 ∙ 6 = 2 ∙ 9
18 = 18 tačno
b) 18 : 24 = 3 : 4
⇒ 18 ∙ 4 = 24 ∙ 3
72 = 72 tačno
v) 9 : 11 = 11 : 9
⇒ 9 ∙ 9 = 11 ∙ 11
81 = 121 netačno
Ovaj poslednji primer nam govori da nikad ne smemo menjati mesta brojevima u razmeri jer se uvek mora znati koji je prvi a koji je drugi njen član.
Navešćemo još neke osobine proporcija.
Osobine proporcije:
Primer Reši proporciju:
2./109. strana
g)
d)
e)
Domaći zadatak:
1. Pronađite u kući primer razmere i objasnite kako biste rešili neki problem u vezi s njom: da li recept za pravljenje nekog rastvora pa napišite kako biste ga napravili; ili kako biste napravili umanjeni komad nameštaja, u kojoj razmeri, sa stvarnim merama i merama vašeg modela...
2. U vašoj svesci na kvadratiće nacrtajte neku jednostavnu sliku (recimo glavu mace ali uprošćenu, koristite geometrijske oblike) a zatim sliku ponovite pored ali umanjenu ili uvećanu u nekoj razmeri i obavezno napišite u kojoj razmeri. Uz pomoć kvadratića u svesci ćete lakše povećati sve dužine na crtežu nekoliko puta. Videćemo koliko ćete biti uspešni 🎨🖌 Ovo je korisna vežba, na isti način sam i ja na milimetarskoj hartiji nacrtala crtež koji sad uvećan vidite iznad vrata pored učionice za ruski jezik. Nije bilo potrebe crtati veliki crtež već samo nacrtati željeni mali a posle samo meriti lenjirom i kopirati uvećane dužine. Pokušajte!
3. Uprostite razmere (nek im članovi budu prirodni, uzajamno prosti brojevi):
a) 0,12 : 0,036 b) (8 celih 3/4) : (4 cela 1/12)
uradite iz školske zbirke sa strane 109. zadatke: 2. a), b), v), đ) i 3.



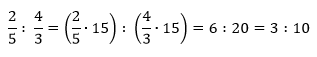











Comments
Post a Comment