Površina kružnog prstena

Kružni prsten je, kako mu i ime kaže, figura koja je ograničena sa dva koncentrična kruga, neko kaže i venac a liči i na točak. Naš zadatak će biti da mu izračunamo površinu. Kako ćemo to da uradimo? Jednostavno, zamislite da sa mamom pravite kolače kružnog oblika koji treba da imaju rupu u sredini. Kako ih pravite, tj. kako oni nastaju? Tako što modlom od testa odvojite veliki krug koji će vam predstavljati kolač pa mu drugom manjom modlom izvadite sredinu. To je recept i za izračunavanje površine kružnog prstena.

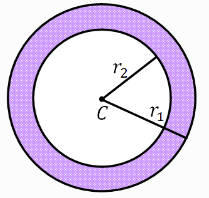
Ako sa r₁ označim poluprečnik većeg kruga a sa r₂ poluprečnik manjeg kruga (ja često volim da koristim i oznake sa indeksima v i m, onda znam uvek na koji krug mislim, veći ili manji, vi možete kako želite), površine njihovih krugova ću računati 

P₁ = r₁²∙ℼ  i   P₂ = r₂²∙ℼ  a površina prstena koji nastaje od ta dva kruga računam po formuli:

Obim prstena računam kao dužinu svih kružnih linija koje ga okružuju tj. prosto:

Op = O₁ + O₂

Zadaci iz ove lekcije su u vašim školskim zbirkama na strani 138.

1. v) r₁ = √3,   r₂ = √2,   Pp = ?

        Pp = P₁ - P₂                         P₁ = r₁²ℼ = (√3)²ℼ = 3ℼ         P₂ = r₂²ℼ = (√2)²ℼ = 2ℼ

                                                    Pp = 3ℼ - 2ℼ = ℼ

3. Pp = 48ℼ cm²       r₂ = 4 cm,   O₁ = ?,    P₁ = ?

    Ništa lakše. Ako imamo poluprečnik manjeg kruga, možemo da izračunamo njegovu površinu:

         P₂ = 4² ∙ ℼ = 16ℼ cm²   a kako je Pp = P₁ - P₂, dobijamo

         48ℼ = P₁ - 16ℼ     ⇒      P₁ = 48ℼ + 16ℼ = 64ℼ,  a znamo da je P₁ = r₁²ℼ, 

                                                                                                           64ℼ = r₁²ℼ   ⇒  r₁ = 8 cm

    Zato je O₁ = 2r₁ℼ = 16ℼ cm

5. razlika poluprečnika je 7 cm   ⇒   r₁ - r₂ = 7 cm

    a njihov zbir je 17 cm              ⇒   r₁ + r₂ = 17 cm

Možemo sad da pokušamo da odredimo poluprečnike, da nagađamo možda, ali nema potrebe.

Pogledajte šta smo malopre zaključili o formuli i razlici kvadrata:

Pp = (r₁ - r₂)∙(r₁ + r₂)ℼ

Pp = 7 ∙ 17ℼ = 119ℼ cm²

Jednostavno, zar ne?

Na sličan način, igranjem sa formulama, pokušajte sami da uradite zadatak broj 6.

8. Prečnik saobraćajnog znaka će sigurno predstavljati veliki prečnik odnosno R₁ = 2r₁ = 80 cm.

    Zadata vam je širina crvene boje. Ta crvena boja je u stvari kružni prsten i zadata vam je njegova        širina. Širina kružnog prstena predstavlja razliku poluprečnika:  r₁ - r₂ = 5 cm. Traži nam se                  površina prstena.

    Zadatak je sad već poprilično jednostavan: iz velikog prečnika zaključimo da je r₁ = 40 cm, a da iz širine da je r₂ manje za 5 cm, tj. r₂ = 35 cm. Sada sami izračunajte površinu prstena.

10. zadatak ponovo iz jednakostraničnog trougla i opisane i upisane kružnice, polako se prisetimo formula:

Domaći zadatak: osim zadataka koje ste dobili da završite, sa strane 138. uradite još i: 1, 2, 4, 7, 9. v) i 11.