Linearne jednačine sa dve nepoznate i sistemi – ponavljanje
Ponavljamo šta smo to naučili iz prethodne dve lekcije. Ko želi, može da pogleda TV lekciju u vezi sa ovim časom na ovom linku.
Zbirka, strana 107.
1. v) Da li je uređeni par (-2, 5) rešenje jednačine: 2y + 3x = 11?
Zamenimo vrednosti i proveravamo tačnost jednakosti (vodi računa o tome koja je prva koordinata, a koja druga).
2*5 + 3*(-2) = 11
10 - 6 = 11
4 = 11
Kako jednakost nije tačna, uređeni par (-2, 5) nije rešenje ove jednačine.
2. g) Odredimo drugu koordinatu rešenja ako znamo da je prva x = 3, tj. da je rešenje naše jednačine (3, y).
4. v) Odredimo vrednost parametra a u jednačini ako znamo da je njeno rešenje (-5, -2).
Iskoristićemo da prilikom zamene rešenja u jednačinu treba da dobijemo tačnu jednakost, pa ćemo lako rešavanjem dobijene jednačine u kojoj ćemo imati samo nepoznatu a doći do našeg odgovora.
5. v) Zadatak nam je da nađemo tri uređena para koja su rešenja jednačine 2x + 3y = 12.
Biramo jednu vrednost recimo za promenljivu x i izračunavamo promenljivu y (kao pri određivanju parova za crtanje grafika linearne funkcije što ova jednačina u stvari i jeste).
1) x = 0 ........ 2*0 + 3y = 12
3y = 12
y = 4 pa je jedno rešenje: (0, 4)
2) x = 3 ....... 2*3 + 3*2 = 12
y = 2: (3, 2)
3) y = 0 ...... 2x + 3*0 = 12
x = 6: (6, 0)
Rešimo i jedan sistem grafičkom metodom tako što ćemo zadate jednačine zapisati u eksplicitnom obliku, nacrtati njihove grafike i pročitati rešenje sistema kao presečnu tačku tih grafika.
Radimo na primeru zadatka 3. b) sa strane 108. vaše zbirke.
2x + 1 = y
2x + y = 1 /-2x
Y = 2x + 1
Y = -2x +1
Biramo vrednosti za x i računamo vrednosti za y za svaku funkciju i na taj način dobijamo sledeće tačke za svaku od funkcija:
prva funkcija: (2, 5), (1, 3)
druga funkcija: (1, -1), (2, -3)
Nacrtamo njihove grafike i pročitamo koordinate presečne tačke koja će biti rešenje sistema. Grafik prve funkcije je crven, grafik druge je plav.
Rešenje našeg sistema je tačka sa koordinatama (0, 1) i zato je naš sistem saglasan (imamo jedno rešenje).
Za vežbu uraditi primere pod v) i g) istog zadatka i prokomentarisati rešenje i tip sistema.
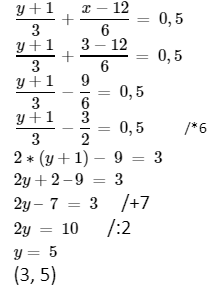




Comments
Post a Comment