Stepenovanje - vežbe I
Uvežbavamo sređivanje izraza sa stepenima uz pomoć sledećih osobina:
20. g) Uprosti izraz:
Poslednji korak je da prepoznamo stepen sa osnovom x i u brojiocu i u imeniocu i da razlomačka crta označava deljenje pa stepene sa istim osnovama možemo da podelimo oduzimanjem izložilaca (osobina 3.). Tako sredimo i stepene sa y u osnovi.
21. Odredi x znajući da je x³ = 27, x⁵ = 32 i x⁵ = 3125.
Ovo su jednačine. Nepoznata može biti u osnovi kao što je ovde ili u izložiocu (pa se tada takva jednačina zove ekponencijalna jer je eksponent = izložilac).
Kako rešavamo takve jednačine? Cilj je na neki način da desnu stranu jednačine napišemo u obliku stepena koji liči na stepen sa leve strane u ovom slučaju. To radimo rastavljanjem zadatih brojeva na proste činioce.
a) x³ = 27
27 = 3 · 3 · 3 = 3³
x³ = 3³
Kako smo napravili iste izložioce, a već u samoj jednačini piše da je stepen sa leve strane jednak stepenu sa desne strane, logičan je zaključak da i osnove moraju biti jednake pa je x = 3.
x³ = 3³ ⇒ x = 3
Probajte na isti način da rešite i druge dve jednačine a slede rešenja...
b) x⁵ = 32
32 = 2 · 2 · 2 · 2 · 2 = 2⁵
x⁵ = 2⁵ ⇒ x = 2
v) x⁵ = 3125
3125 = 5 · 5 · 5 · 5 · 5 = 5⁵
x⁵ = 5⁵ ⇒ x = 5
Probajte sami da rešite i sledeća dva primera sa strane 134.: zadatak 18. e) i ž).
Rešenja proverite ispod.
18. e)
ž)
Rešenja prošlog domaćeg sa strane 126.:
14. đ) a²⁹; z) b³⁰; j) z.
15. a) a⁴⁰ ; v) x⁶ .
20. a) a⁹; b) b⁸; v) p²; d) 3¹⁰/(x⁵y¹⁰); đ) x+1.
Za vežbu probati zadatke: 18./strana 126, 27./strana 128, 17./strana 134. i 23./strana 134.
18. Uputstvo: nemojte stavljati * već stepen sa istom osnovom, znači x, a izložilac n, pa će cilj biti naći n. Primer d):
Pa je * = x.

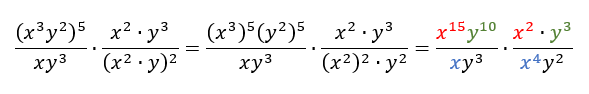
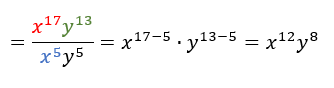






Nice one
ReplyDelete